Population Structure
Hey, nice to see that you are interested in the functionality behind the automated creation of tracks. In the following the most important aspects and principles used are explained. It helps if you already had contact with optimization but it should be also understandable if you got no previous knowledge whatsoever.
The intended purpose of this text is to inspire you to take on your own ideas. Most problems are easily solvable without rocket science. Sometimes it just takes a little nudge in the right direction.
Goal of the track generator is the creation of a track which meets defined criteria. This means we have an optimization problem with the goal of finding the best track possible. One way to solve optimization problems is with metaheuristics. Metaheuristics are algorithms used for solving optimization problems which are not trying to find the optimal solution, but instead just try to find a solution which is sufficient. While we want to find a good track, we don't need to find the best track there is (if there is even a thing like an optimal track).
One type of metaheuristic are evolutionary algorithms, which are used here. Evolutionary algorithms are inspired by biological evolution in the nature. Processes like mutation, selection, recombination and reproduction are transferred into the form of algorithms. Notably for this algorithm is the introduction of randomness in the solution process like in it's biological archetype. This fact is important, because most algorithms are deterministic, which means that with a given input the algorithm always returns the exact same solution. If you start in contrast an evolutionary algorithm with the same parameters, you will never get the same solution on different run throughs.
So why do we use evolutionary algorithms in this particular problem? There are two reasons: First; through the non-deterministic nature of the algorithm we can create an unlimited number of different tracks. Second; evolutionary algorithms are useful in problems where you know how a good solution looks like but you don't know how to reach it (efficiently).
The evolutionary algorithm is structured as followed:
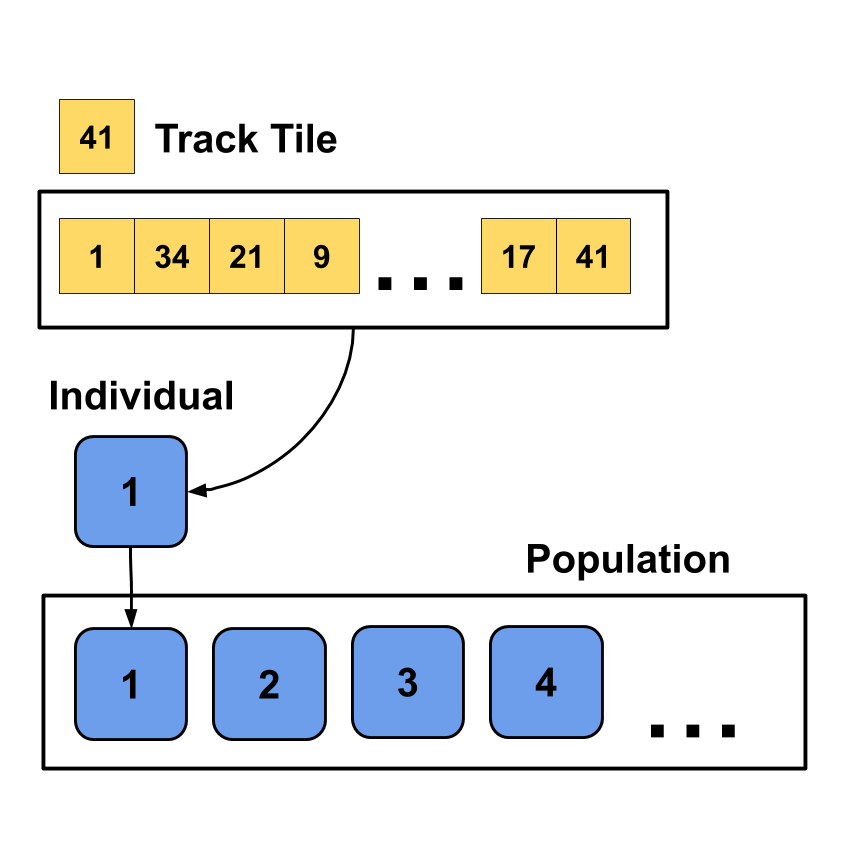
A track is the base element of the algorithm. It consists of ordered, numbered track tiles. One created track is called an individual in the algorithm. One core concept of the evolutionary algorithm is the existence of not only one individual, but a whole population of individuals. This accumulation of individuals is equivalent to a gene pool in the nature. We try to hold this pool as variable as possible so the evolution can thrive. The pool of individuals itself is called the population.
First step of the algorithm is the initialization of the population. At the start of the algorithm the number of individuals in the population is defined. The size of the population doesn't change over the evolutionary process. Higher number of individuals can lead to a faster solving of the algorithm but also need more computing power.
Every individual of the initial population gets a randomly ordered selection of usable track tiles. Only the first tile is defined to be a start tile and the last tile is fixed to be the finish tile. Generally, you want the initial creation of the individuals to be as randomly as possible. Often humans have assumptions regarding the composition of the initial population and therefore can skew the evolutionary process if they implement these assumptions. Thus, the solution space is reduced and possible solutions can't be reached. Instead just trust the evolutionary process.

Centerpiece of the evolutionary algorithm is the fitness function. The fitness function is used to evaluate and compare individuals.
The following simple example explains how the fitness function works and why do you want to use it. Imagine you want to play a game of Flamme Rouge. You like the tactical aspect of ascents so there should be quite a number of ascents in the track. Furthermore, the table you play on is quadratic so the track needs to fit on there. Other factors like descents, cobblestones or breakaway tiles are not important to you.
Just from this information you can be shown four different tracks and you would have no problems ordering them regarding the likelihood you would select them. If you see the following four tracks you instantly can decide which track would be the best for your situation.
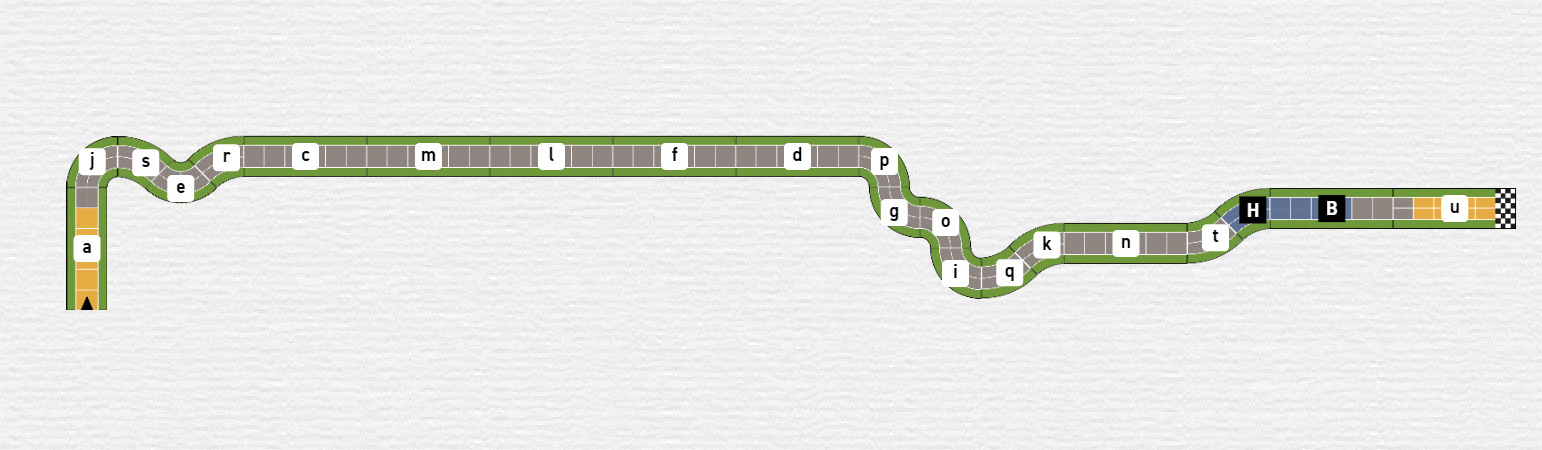
Track 1 does not fit any of your criteria. The track is super long stretched and would therefore fall off both sides of your table. No ascents are included so it is also boring for you to play. You would not select this track.
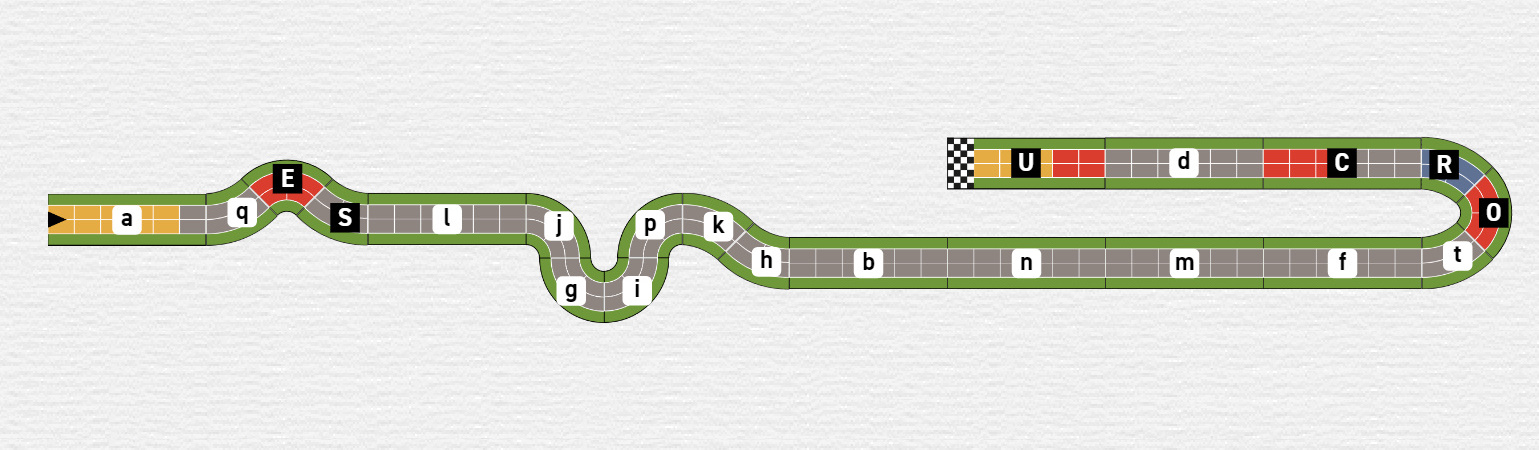
Track 2 instantly draws more attention from you than track 1. You see lots of little ascents and you can already feel the suspense it would bring in a tight race near the finish line. Unfortunately, this track is also way to big for your table, so while you like the track you would look out for a different option.
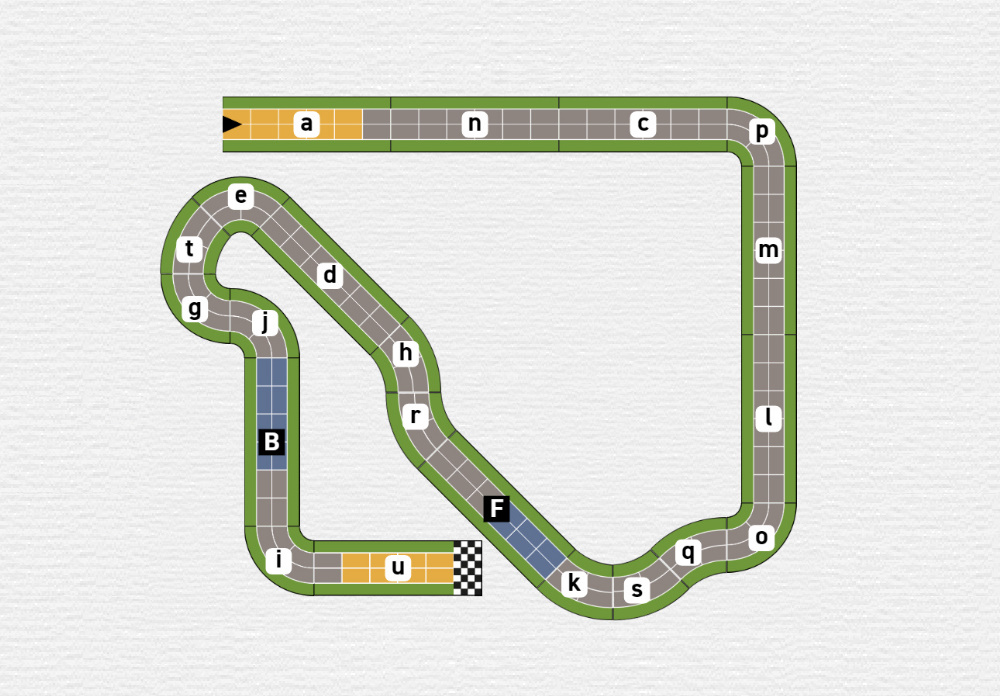
When you see track 3 you can breathe a sigh of relief. So, there are tracks which fit on your super pretty table, like your significant other said, while you asked yourself why people even produce tables that small. Gameplaywise there are no ascents at all, so you put all your hope in track number four.
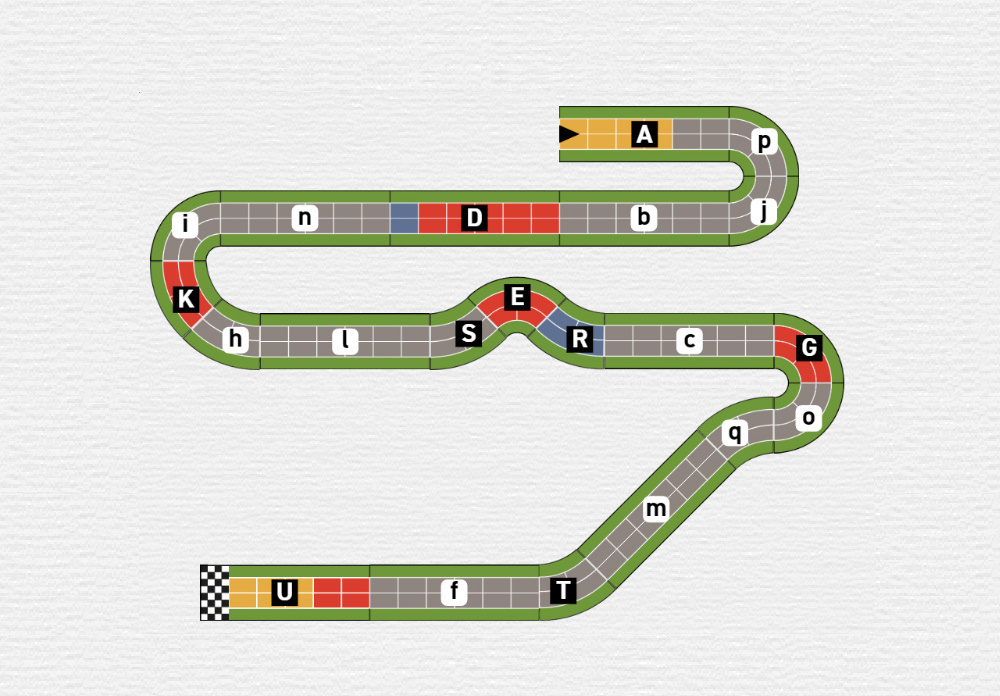
One glance at track 4 and you know you've found what you've been looking for. It fits all your requirements. It has lots of ascents and even will fit on your table. You would instantly select this track.
The given example shows the principles of the fitness function. You define criteria with which you can evaluate how good an individual is. These criteria are formalized into the fitness function.
A fitness function calculates a fitness value for a given individual. Because we use a minimizing function here, an individual which fulfills all sought after criteria has a fitness value of zero. If we find such an individual, the goal of the evolutionary algorithm is fulfilled and we have a track to present to the user. Each criterion which is not fulfilled however returns a penalty value. For every individual the fitness values are stored to be used in the next step.
Two of the criteria, or parts of them, were shown in the example. The criteria used can be ordered into two classes. One class evalutes the physical dimensions of the track, the other class evalutes the properties of the track.
For instance, there are two criteria regarding the physical dimensions of a created track. One criterion compares the length and width of the track with the given selection of the user. Another criterium is needed to check if the physical layout of the track is acceptable. Because if you randomly order track tiles together it can happen that the track overlaps. So your track could be within the selected dimensions but would be unplayable at the same time. Therefore, every track is physically simulated and checked for overlaps in the track.
All other criteria are involved with the properties of the created track. So is the number of ascents, descents or cobblestone tiles compared to the selected values of the user, like shown in the example. Another criterium evalutes the layout and ordering of the track tiles.
Generally, it is possible to create a lot of different criteria for the fitness function, but it is best to limit them to the ones really needed. Aspects like the correct start and finish tiles or a check for doubled tiles could also be implemented. But for these it is easier and more practicable to already handle them in the track creation process.
With the evaluation of the fitness function all individuals can now be ranked regarding their fitness. This is needed because only the fittest individuals will stay in the evolution process. Bad individuals will be dropped from the pool to make room for potential better individuals.
The selection of the fittest individuals is done with the NSGA-II algorithm. Because we have multiple criteria which are evaluated in the fitness function, the selection algorithm needs to be able to handle multi-objective optimization. NSGA-II orders all individuals in pareto fronts and orders them regarding their crowding distance. Afterwards the best individuals are selected to be retained. The next images show the principles of the algorithm.
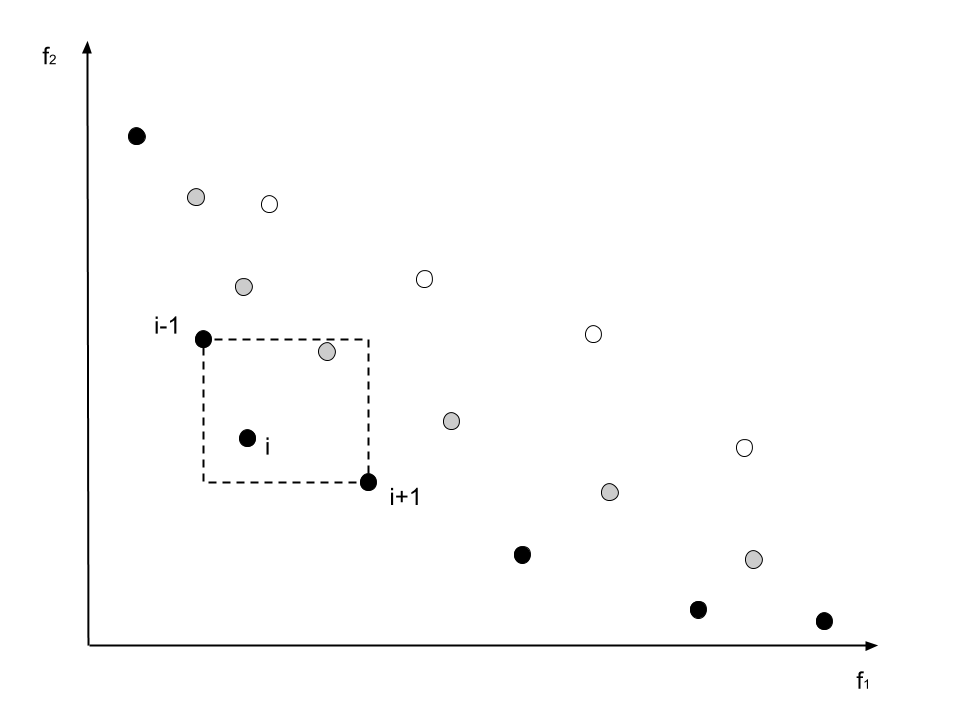
The graph shows the exemplary sorting of individuals into pareto fronts. The black individuals are all non-dominated and therefore the best individuals. For every individual in the front the distance to it's neighbours is messured. The more isolated an individual is, the better it is ranked inside it's front.
The gray points build the new front if the black individuals are removed. The white individuals are the third front.
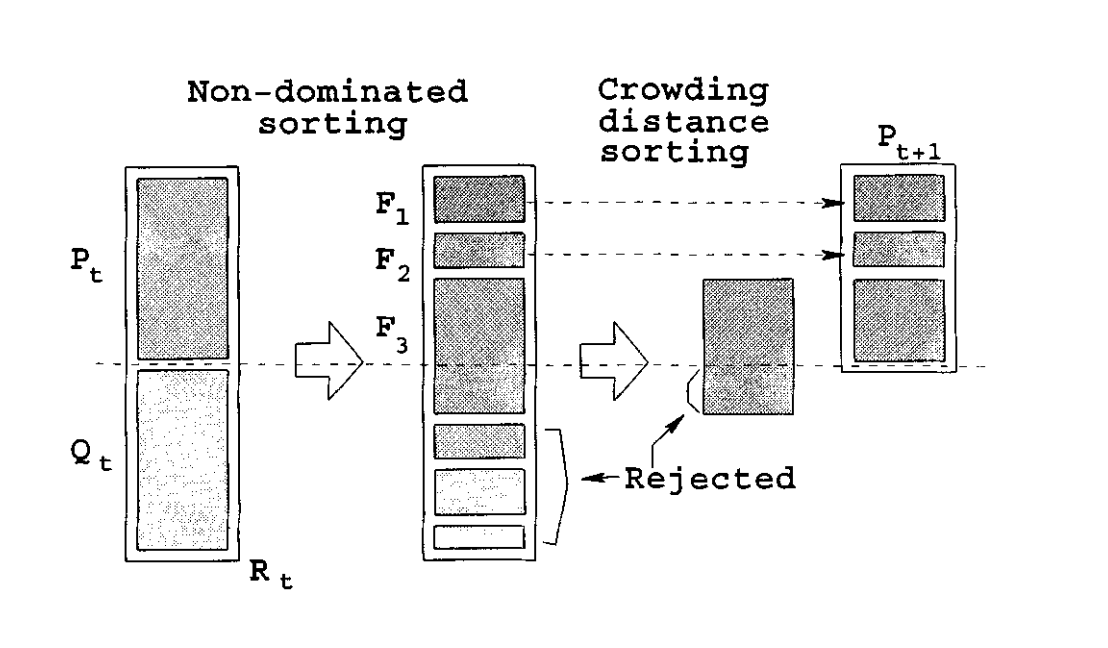
After the sorting into the pareto fronts and the ordering regarding the crowding distance, the best individuals are selected.
Source: [1]
With the selection of the fittest individuals the algorithm begins its evolutionary part. The evolutionary process is done in generations. Each generation starts with the selected best individuals of the last generation. These are passed into the next generation. All the spots of the rejected individuals are filled with clones of the selected individuals. When the original population size is reached again, the individuals in the population evolve.
The evolution of the individuals is done via mutation. Mutation is the random alteration of the "genome" of an individual. The genome of an individual is its ordered set of track tiles. This set of track tiles is altered through a selection of operations. Single or groups of track tiles can be flipped, switched, scrambled, inversioned or swapped. It is also possible to reintroduce track tiles currently not used.
All these mutations are done randomly. Like in nature this can have positive, negative or no effects at all. We just hope that through the mutation some individuals improve and therefore push the population closer to the desired meeting of the criteria.
With the mutation all needed steps for the evolutionary algorithm are introduced. From this point on, the algorithm runs through an iterative cycle.
After the mutations the individuals of the population evolved and changed. Therefore, a new evaluation via the fitness function is necessary. Should an individual reach a fitness value of zero the algorithm would conclude. All criteria would have been met and the track would be returned to the user.
If no individual has a fitness value of zero the algorithm continues. In continuation of the iterative cycle, the best individuals are selected, transferred into the next generation and then mutated again. The iteration has two termination conditions. First is the addressed fitness value of zero. Second termination condition is the achievment of a specified number of maximum generations. If the criteria can't be met, the algorithm would run endlessley otherwise. It is also possible that the population evolved into a state from which it can't improve, but is also not good enough to meet the set criteria.
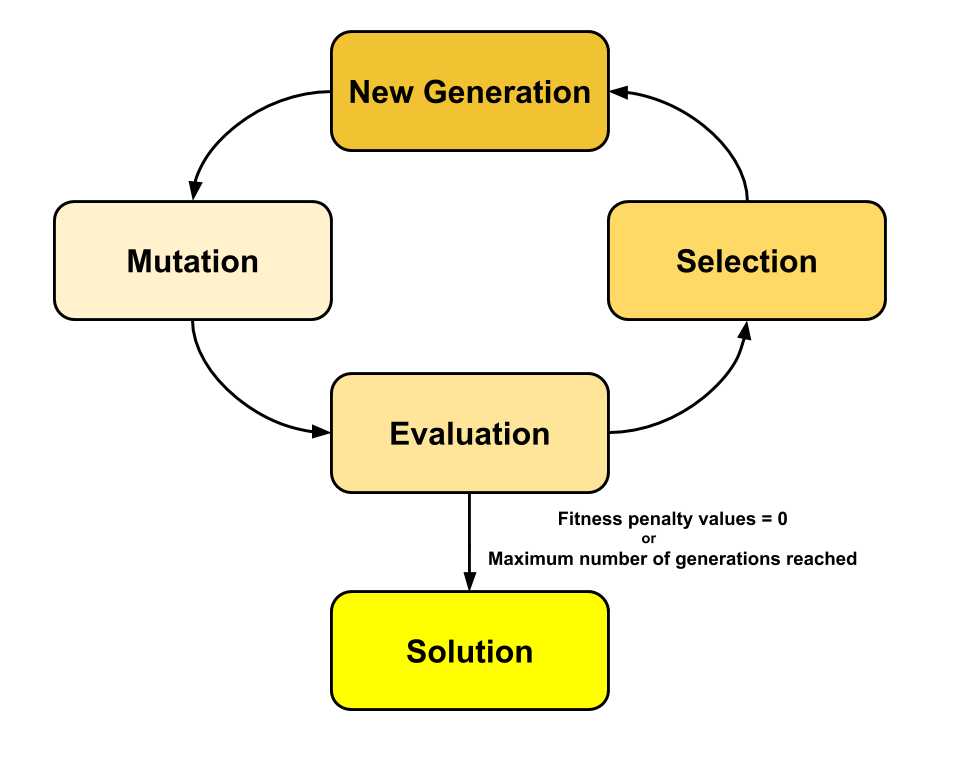
The iterative cycle of the evolutionary algorithm runs until either a viable solution is found or the maximum number of generations is reached. If the algorithm ends through the generation break condition, no optimal solution has been found. In this case the best-found solution up to this point is returned.
This is the process which is behind the automated track generation. Hopefully you learned something or got an idea for your own problem. Check out the listed book of Luke (2013) for an overview of metaheuristics and an entry into the topic.
[1] K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, "A fast and elitist multiobjective genetic algorithm: NSGA-II," in IEEE Transactions on Evolutionary Computation, vol. 6, no. 2, pp. 182-197, April 2002, doi: 10.1109/4235.996017.
If you are interested in the topic of optimization and metaheuristics, have a look at the following book. It is free, super well written and has lots of pseudocode examples:
Sean Luke, 2013, Essentials of Metaheuristics, Lulu, second edition, available at http://cs.gmu.edu/~sean/book/metaheuristics/